Skillnad mellan versioner av "Fasjämvikter"
Per (Diskussion | bidrag) |
Per (Diskussion | bidrag) (→Clapeyrons ekvation (alla fasövergångar)) |
||
| Rad 42: | Rad 42: | ||
:<math>\left(\frac{\partial p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} H_m}{T\Delta_{\alpha\rightarrow\beta} V_m}</math> | :<math>\left(\frac{\partial p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} H_m}{T\Delta_{\alpha\rightarrow\beta} V_m}</math> | ||
| − | Ekvationen kan exempelvis användas för att beräkna hur ett ämnes smältpunkt beror på trycket. Eftersom <math>\Delta_{ | + | Ekvationen kan exempelvis användas för att beräkna hur ett ämnes smältpunkt beror på trycket. Eftersom <math>\Delta_{s\rightarrow l} H_m</math> alltid är positiv är det tecknet på volymsändringen som påverkar i vilken riktning smältpunkten ändras. För de flesta ämnen har vätskan större molvolym än den fasta fasen, vilket gör att smältpunkten stiger med ökande tryck. För vatten har som bekant den fasta fasen större molvolym än vätskan, vilket gör att smältpunkten tvärtom sjunker med ökande tryck. |
== Clausius-Clapeyrons ekvation (ena fasen gas) == | == Clausius-Clapeyrons ekvation (ena fasen gas) == | ||
Nuvarande version från 8 januari 2019 kl. 11.55
En konsekvens av andra huvudsatsen är att vid jämvikt så är den kemiska potentialen för ett ämne lika i hela systemet, oavsett hur många faser som finns. Om den flytande och fasta fasen av ett ämne står i jämvikt med varandra är alltså den kemiska potentialen för ämnet lika i båda faserna. För att se detta, antag att den kemiska potentialen är högre i vätskefas än i fast fas, Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu^l>\mu^s} , och titta på processen då en liten mängd, Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dn} , överförs från vätska till fast fas. Summan av ändringen i Gibbs energi för vätskan och det fasta ämnet ges då av
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dG=dG_l+dG_s=-\mu^l\,dn+\mu^s\,dn=(\mu^s-\mu^l)\,dn<0}
där den sista olikheten följer av antagandet Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu^l>\mu^s} . Processen, att molekyler överförs från vätskan till den fasta fasen, är alltså spontan eftersom den ger en negativ ändring i Gibbs energi. Jämvikt (d.v.s. att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dG=0} ) kräver alltså att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu^l=\mu^s}
Clapeyrons ekvation (alla fasövergångar)
Antag att vi är vid en punkt (p, T) där jämvikt råder mellan två faser Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha} och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta} . Detta betyder alltså att vi befinner oss på någon av linjerna (fasgränserna) i det "vanliga" fasdiagrammet:
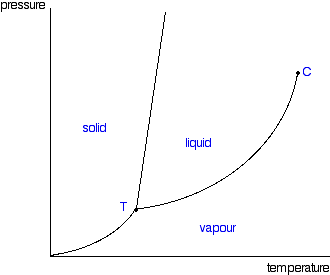
Enligt ovan gäller
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu^\alpha(p,T)=\mu^\beta(p,T)\;\;\;\;\;} (1)
där vi förtydligat att den kemiska potentialen beror på tryck och temperatur.
Vi frågar oss nu på vilket sätt vi kan ändra p och T så att jämvikt fortfarande gäller, d.v.s. att vi "följer linjen" i fasdiagrammet. En sådan ändring måste ju uppfylla
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\mu^\alpha=d\mu^\beta}
eftersom (1) ska gälla både före och efter ändringen. Men vi vet från avsnittet om tryck- och temperaturberoende för Gibbs energi att
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\mu^\alpha=V_m^\alpha\,dp - S_m^\alpha\,dT}
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\mu^\beta=V_m^\beta\,dp - S_m^\beta\,dT}
där vi använt att kemiska potentialen är detsamma som molär Gibbs energi för vardera fasen, eftersom varje fas här består av en enda komponent. Kombination av de tre senaste ekvationerna ger
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_m^\alpha\,dp - S_m^\alpha\,dT=V_m^\beta\,dp - S_m^\beta\,dT}
vilket kan förenklas till
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(V_m^\alpha-V_m^\beta\right)\,dp = \left(S_m^\alpha- S_m^\beta\right)\,dT}
Detta är alltså det samband som måste gälla mellan tryck- och temperaturändringarna Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dp} och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dT} för att jämvikten ska bibehållas. Om vi inför beteckningen Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta}} för differensen mellan Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta} och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha} och "dividerar" differentialerna för att få en derivata, erhålls Clapeyrons ekvation:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} S_m}{\Delta_{\alpha\rightarrow\beta} V_m}}
där vi specificerat "riktningen" på den partiella derivatan genom att säga att jämvikten ska bibehållas, istället för att som vanligt hålla en variabel konstant (vi skulle här i och för sig ha kunnat säga att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta} \mu} skulle vara konstant).
Eftersom vi vet att för en reversibel fasövergång (alltså vid jämvikt) gäller att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta} S_m = \Delta_{\alpha\rightarrow\beta} H_m / T} kan vi också uttrycka Clapeyrons ekvation så här:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} H_m}{T\Delta_{\alpha\rightarrow\beta} V_m}}
Ekvationen kan exempelvis användas för att beräkna hur ett ämnes smältpunkt beror på trycket. Eftersom Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{s\rightarrow l} H_m} alltid är positiv är det tecknet på volymsändringen som påverkar i vilken riktning smältpunkten ändras. För de flesta ämnen har vätskan större molvolym än den fasta fasen, vilket gör att smältpunkten stiger med ökande tryck. För vatten har som bekant den fasta fasen större molvolym än vätskan, vilket gör att smältpunkten tvärtom sjunker med ökande tryck.
Clausius-Clapeyrons ekvation (ena fasen gas)
Om den ena fasen (låt oss säga Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta} ) är gas kan vi approximera volymsändringen enligt följande:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta} V_m \approx V_m^g \approx \frac{RT}{p}}
I den första approximationen försummar vi alltså molvolymen för den kondenserade fasen eftersom gasens molvolym är så mycket större. I den andra approximationen antar vi att gasen beter sig idealt. Insättning av detta uttryck i Clapeyrons ekvation ger
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1}{p}\left(\frac{\partial p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} H_m}{RT^2}}
Genom kedjeregeln ser vi att vänsterledet även kan skrivas som en derivata av Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln p} :
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial \ln p}{\partial T}\right)_{\alpha \rightleftharpoons \beta} = \frac{\Delta_{\alpha\rightarrow\beta} H_m}{RT^2}}
Clausius-Clapeyrons ekvation kan användas för att beräkna hur ett ämnes kokpunkt beror på trycket, eller omvänt hur ångtrycket beror på temperaturen. I specialfallet att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta} H_m} kan antas vara konstant i det aktuella temperaturintervallet kan differentialekvationen lösas med variabelseparation och vi får:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln\frac{p_2}{p_1}=\frac{\Delta_{\alpha\rightarrow\beta} H_m}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)}
Observera att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{\alpha\rightarrow\beta} H_m} är samma sak som Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{vap} H} om vi tittar på övergången från vätska till gas. Om vi har uppmätt Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} för många punkter kan vi använda linjär regression för att bestämma Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{vap} H} .