Adsorption
Innehåll
Tillsatsers inverkan på ytspänningen
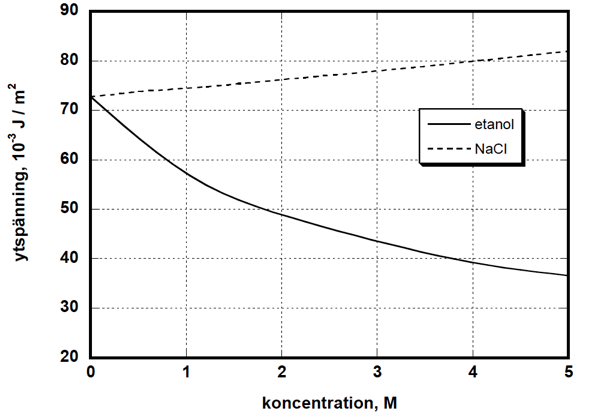
Experiment visar att när ämnen som har starka intermolekylära interaktioner med omgivande H2O-molekyler tillsätts till en vattenlösning så höjs som regel lösningens ytspänning. Exempel på sådana ämnen är enkla salter, starkt polära ämnen och ämnen med många OH-grupper. Om däremot ett opolärt ämne, eller ett ämne som innehåller en stor opolär del, tillsätts till en vattenlösning sänks som regel lösningens ytspänning (se figur 1)
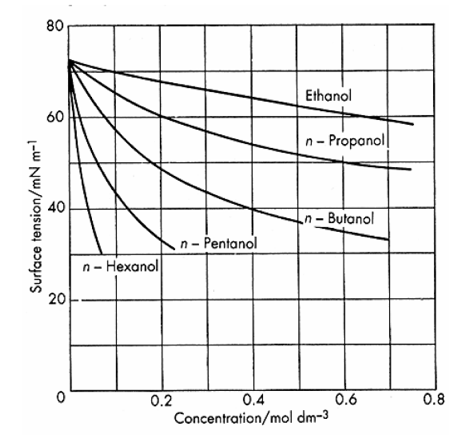
När vissa ämnen tillsätts till en vattenlösning
kan även en mycket liten tillsatts ge en
dramatisk sänkning av lösningens ytspänning.
Ämnen som uppvisar denna egenskap kallas
ytaktiva ämnen, se t.ex. n-hexanol i figur 2.
Att ytspänningen på en lösning beror på
lösningens sammansättning är inte så
konstigt. Som vi såg tidigare är det
förändringen i fri energi för de molekyler
som tvingas att vara i gränsskiktet till en
lösning, Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta\mu_{yta}}
, som ger upphov till lösningens
ytspänning. För en lösning som innehåller
flera olika komponenter innebär detta att det
är summan av förändringarna i fri energi för
de olika molekyler som är placerade i
lösningens ytskikt, som ger upphov till lösningens ytspänning:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma = \sum_i \frac{n_{i,yta}}{\cal{A}}\cdot\Delta\mu_{i,yta}}
Detta betyder att man måste känna till både Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta\mu_{i,yta}} och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{i,yta}} för varje komponent för att kunna beräkna ytspänningen. En förenkling skulle här kunna vara att man ansatte att ytskiktet har samma sammansättning som bulklösningen. Detta antagande leder till ett linjärt samband mellan lösningens sammansättning och dess ytspänning. Ansatsen är emellertid i de flesta fall mycket dålig, se figur X. Som regel avviker sammansättningen i ytskiktet till en lösning kraftigt från bulklösningens sammansättning.
Molekylfördelningen mellan bulkfasen och ytan
Det som karakteriserar en vattenlösning är dels den starka intermolekylära interaktionen mellan H2O-molekylerna ( vätebindningar och dipol–dipol interaktioner ), dels den starka interaktionen mellan H2O-molekyler och upplösta joner och andra starkt polära molekyler. Om en opolär molekyl skall ta sig in i denna miljö är det energetiskt ogynnsamt eftersom flera H2O-H2O ”bindningar” kommer att störas, eller försvinna, i en sådan process. Om den opolära molekylen däremot placeras vid lösningens gränsyta mot luft behöver inte så många H2O-H2O ”bindningar” störas för att skapa utrymme åt den upplösta molekylen.
För en upplöst jonisk eller starkt polär molekyl är effekten den motsatta, det är energetiskt ogynnsamt att placera dessa molekyler i gränsytan mot luft.
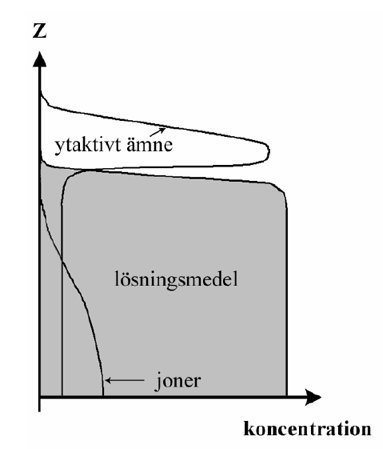
Denna skillnad i de lokala intermolekylära interaktionerna, mellan ett upplöst ämne och omgivande molekyler i ett gränsskikt respektive i en bulklösning, leder till att koncentrationen av det upplösta ämnet inte är densamma i gränsskiktet som i det inre av den intilliggande bulklösningen. För opolära ämnen erhålles en högre koncentration i vattenytan jämfört med bulklösningen, medan joniska eller starkt polära ämnen i de flesta fall uppvisar en lägre koncentration i närheten av vattenytan jämfört med bulklösningen, se figur 2.
Som framgår av figur 2 kan den lokala koncentrationen av joner avvika från bulkkoncentrationen även på ganska stora avstånd från gränsytan, medan koncentrationen av andra upplösta ämnen endast avviker från bulkkoncentrationen i ett mycket tunt ytskikt.
För att fullständigt kunna beskriva en ytregions olika kemiska och fysikaliska egenskaper är det nödvändigt att i detalj känna till hur koncentrationen av lösningsmedlet och varje upplöst ämne varierar som funktion av avståndet till lösningens gränsyta. Effekten på en lösnings ytspänning av en tillsatts av j-molekyler till lösningen beror emellertid endast på hur många fler, eller hur många färre j-molekyler, jämfört med koncentrationerna av j-molekyler i omgivande faser, som finns i området kring gränsytan. Denna storhet kallas ytöverskottet av ämnet j och betecknas oftast med Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_j} :
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_j=\frac{\Delta n_{j,yta}}{\cal{A}}}
I ovanstående samband betecknar Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta n_{j,yta}/\cal{A}} överskottet, eller underskottet, av j-molekyler per ytenhet av den aktuella gränsytan. Med överskott menas antalet mol j-molekyler som finns i det aktuella gränsskiktet minus hur många j-molekyler som skulle finnas i motsvarande område om koncentrationen inom respektive fas var konstant. Om vi mäter hur den lokala koncentrationen av j varierar med avståndet från ytan, t.ex. genom neutrondiffraktion, kan vi i princip räkna ut vad Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_j} blir, men vanligare är att man använder mätning av ytspänningen för att dra slutsatser om fördelningen istället.
Gibbs adsorptionsekvation
I avsnittet 2-2 framkom att ämnen som ger ett positivt ytöverskott i en lösning sänker lösningens ytspänning, medan ämnen som ger ett negativt ytöverskott (= ytunderskott) höjer ytspänningen. Ett mera kvantitativt samband för de observerade effekterna ges av Gibbs adsorptionsekvation. Enligt Gibbs adsorptionsekvation ger en förändring av koncentrationen av en komponent B i en lösning, dcB, upphov till en förändring av lösningens ytspänning, dγ, på följande sätt:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{d\gamma}{dc_B}\approx-\Gamma_B\cdot\frac{d\mu_B}{dc_B}}
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_B} är ytöverskottet och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_B} den kemiska potentialen av ämnet B i den aktuella bulklösningen. Den kemiska potentialen för en komponent B i en lösning kan som bekant skrivas som
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_B=\mu_B^\circ + RT\ln \gamma_B\frac{c_B}{c^\circ}}
där γB är aktivitetsfaktorn för ämnet B vid den aktuella koncentrationen och .....en 1M lösning.
För två gränsfall kan den kemiska potentialens koncentrationsberoende och därmed Gibbs adsorptionsekvation lätt beräknas:
I) När lösningen är ideal för ämnet B.
För detta fall är μB = μB (1M) + RT ⋅ ln(cB /1M) vilket leder till följande samband:
Sambandet 2-5b visar att ytöverskottet av ett ämne B i en ideal lösning, ΓB, direkt kan erhållas från ytspänningsdata om ytspänningen plottas som funktion av ln(cB /1M), se figur 2-15. Enligt ekvation 2-5b är lutningen vid koncentrationen cB i en sådan kurva lika med -ΓB(cB) ⋅ RT. Figur 2-15 redovisar ett typiskt beteende på ytspänningens koncentrationsberoende när ett ytaktivt ämne tillsättes till en lösning.
a) Vid låga koncentrationer är lutningen på γ-kurvan nästan noll. Detta betyder att ytöverskottet vid dessa koncentrationer är mycket lågt. En noggrannare analys visar att ytöverskottet vid låga koncentrationer oftast kan skrivas som:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_B=\frac{\gamma_0-\gamma(c_B)}{RT}}
För icke ytaktiva ämnen kan detta sambandet oftast användas inom ett stort koncentrationsintervall, men för ytaktiva ämnen är det giltiga koncentrationsintervallet oftast mycket begränsat.
b) Vid högre koncentrationer blir γ-kurvans lutning alltmer negativ. Vilket betyder att ytöverskottet ökar i detta koncentrationsintervall. Observera emellertid att den negativa lutningen på γ-kurvan blir konstant över en viss B-koncentration. Detta betyder att ytöverskottet här nått ett maximalt värde som inte kan överskridas.
c) Slutligen avstannar förändringen av ytspänningen som funktion av totalkoncentrationen helt. Oftast sker denna förändring inom ett mycket snävt koncentrationsintervall. Orsaken till detta beteende kommer nu att diskuteras.
II) När det sker en fasseparation, eller
micellbildning, i den aktuella lösningen kommer
den kemiska potentialen av B inte att variera
som funktion av totalkoncentrationen så länge
detta sker, se figur 2-16. Detta betyder att
ytspänningen i detta koncentrationsintervall är
konstant.