Ideal lösning
Vi har tidigare sett att tryckberoendet hos den kemiska potentialen för en ideal gas har utseendet:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu(p)=\mu^\circ + RT\ln\frac{p}{p^\circ}}
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu^0} är den kemiska potentialen för gasen vid standardtrycket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p^0=1} bar. Eftersom molekylerna i en blandning av ideala gaser inte växelverkar med varandra överhuvudtaget kommer det nog inte som någon överraskning att vi kan tillämpa ovanstående ekvation även på en gasblandning, om vi byter ut trycket mot partialtrycket:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_A(p_A)=\mu_A^\circ + RT\ln\frac{p_A}{p^\circ}}
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_B(p_B)=\mu_B^\circ + RT\ln\frac{p_B}{p^\circ}}
- etc.
Utseendet på dessa ekvationer stämmer väl överens med den intuitiva slutsatsen vi drog när vi resonerade om kemisk potential när det gällde diffusion och kemiska reaktioner, nämligen att den kemiska potentialen har en del som framför allt beror på molekylens stabilitet, och en del som beror på någon slags effektiv koncentration, i det här fallet partialtrycket. Faktum är att den kemiska potentialen alltid har detta utseende och kan formuleras som
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_i=\mu_i^\circ + RT\ln a_i}
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} är aktiviteten för ämne i. Aktiviteten är en slags effektiv koncentration som kan sägas definieras av den ekvationen. För en del system, som t.ex. ideal gas, blev aktiviteten ett särskilt enkelt uttryck, Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i=p_i/p^\circ} . Vi ska nu titta närmare på det enklaste sådana exemplet när det gäller vätskeblandningar.
Innehåll
Ideal lösning
Vi definierar en ideal lösning som en vätskeblandning där den kemiska potentialen för varje komponent (ämne) uppfyller följande ekvation:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_i\,=\,\mu_i^\circ + RT\ln x_i\;\;\;\;\;} (1)
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i} är molbråket för komponenten i vätskeblandningen som, om vi har två komponenter A och B, ges av:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A=\frac{n_A}{n_A+n_B}}
Med andra ord kan vi säga att för en ideal lösning så är aktiviteten för varje komponent lika med dess molbråk. Vi ska strax se att detta är nästan ekvivalent med att lösningen uppfyller det empiriska sambandet Raoults lag. För att en lösning ska vara (nära) ideal krävs normalt att de ingående ämnena har snarlika egenskaper och till och med att molekylerna är lika varandra. Vi ska senare behandla lösningar där bara den ena komponenten beter sig idealt (uppfyller ekvationen ovan) och vi ska även titta på avvikelser från idealitet.
Raoults lag
Vi frågar oss nu vad partialtrycket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A} blir ovanför en ideal lösning vid en given temperatur T när det råder jämvikt mellan vätskefas och gasfas. För att svara på detta definierar vi Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A^*} som partialtrycket över den rena vätskan A, vilket är detsamma som ångtrycket för vätskan vid temperaturen T eftersom vi även här förutsätter jämvikt. Om vi nu antar att A i gasfas uppför sig som en ideal gas, vet vi från början av det här kapitlet att den kemiska potentialen för A i gasfas beskrivs av:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_A(g)=\mu_A^\circ(g) + RT\ln\frac{p_A}{p^\circ}}
När fasjämvikt råder så måste, för varje komponent, den kemiska potentialen i lösningen vara lika med den kemiska potentialen i gasfas där partialtrycket är Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A} , alltså:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_A(soln)=\mu_A^\circ(g) + RT\ln\frac{p_A}{p^\circ}\;\;\;\;\;\;} (2)
Motsvarande gäller förstås för den rena vätskan A, vars ångtryck är Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A^*} :
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_A(l)=\mu_A^\circ(g) + RT\ln\frac{p_A^*}{p^\circ}}
Men nu vet vi att lösningen är ideal, och därmed gäller
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_A(soln)=\mu_A(l)+RT\ln x_A = \mu_A^\circ(g) + RT\ln\frac{p_A^*}{p^\circ} +RT\ln x_A = \mu_A^\circ(g) + RT\ln\frac{x_A p_A^*}{p^\circ}}
Jämförelse med ekvation (2) ger att
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A = x_A p_A^*}
vilket är Raoults lag. Observera att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A} är molbråket i lösningen, inte i ångan. Vi ser alltså att en egenskap hos lösningen ger upphov till ett samband mellan partialtrycken för ångan som står i jämvikt med lösningen respektive det rena ämnet.
Blandningsentropi
Vi ska nu undersöka hur Gibbs energi ändras när två komponenter blandas till en ideal lösning under konstant tryck och temperatur. I praktiken är det lättast att tänka sig detta som att vi har placerat de två rena ämnena i en behållare på varsin sida om en rörlig skiljevägg och försäkrat oss om att samma tryck och temperatur råder i hela behållaren. Den blandningsprocess vi tittar på är det som inträffar när sedan skiljeväggen tas bort.
Först behöver vi ett uttryck för Gibbs energi för det totala systemet efter att skiljeväggen tagits bort. Eftersom vi skulle kunna bygga upp systemet genom att addera lite i taget av en vätska med konstant proportion gäller:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_{efter}=\sum_i n_i\,\mu_i}
Gibbs energi för systemet före dess att skiljeväggen tas bort får vi genom att bara addera Gibbs energi för delsystemen som består av rena ämnen i motsvarande mängd:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_{innan}=\sum_i n_i \, \mu_i^\circ }
Låt oss nu räkna ut skillnaden i Gibbs energi för blandningsprocessen för en total mängd Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{tot}} av lösningen:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{mix} G=G_{efter}-G_{innan}=\sum_i n_i\,\mu_i-\sum_i n_i\,\mu_i^\circ=\sum_i n_i\,\left(\mu_i-\mu_i^\circ\right)=n_{tot}\sum_i x_i\,\left(\mu_i-\mu_i^\circ\right)}
Insättning av definitionen (1) av ideal lösning ger:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{mix} G = n_{tot}RT\sum_i x_i\,\ln x_i}
Notera att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{mix} G} blir negativ eftersom Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln x_i<0} då Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i<1} . Blandningen är alltså alltid en spontan process. Drivkraften för processen kommer helt från entropiändringen:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{mix} S = -\left(\frac{\partial \Delta_{mix} G}{\partial T}\right)_p = -n_{tot}R\sum_i x_i\,\ln x_i}
vilket alltså är ett positivt tal. Denna entropiändring kallas den ideala blandningsentropin och svarar mot fullständigt slumpmässigt blandande av komponenterna när molekylerna från samtliga komponenter interagerar med varandra på ett identiskt sätt. Det är lätt att se från föregående två ekvationer att
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_{mix} H = \Delta_{mix} G + T \Delta_{mix} S = 0}
så det sker inget värmeutbyte med omgivningen under processen. Även V och U är konstanta under processen.
Eftersom blandningar av ideala gaser kan ses som ideala lösningar så gäller alla dessa uttryck även för gasblandningar.
Fasdiagram (tryck mot sammansättning)
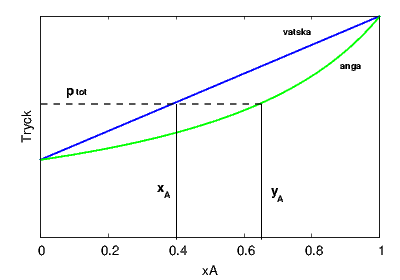
Antag att vi har en ideal lösning med två komponenter A och B. Vi ska plotta två olika kurvor i ett diagram med molbråk av A på x-axeln och tryck på y-axeln. Temperaturen för ett sådant diagram är alltså satt till en konstant. Den ena kurvan är det totala ångtrycket för en blandning med molbråket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A} i vätskan. Detta tryck ges direkt av Raoults lag:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_{tot}=p_A+p_B=x_A\,p_A^* + (1-x_A)\,p_B^*}
där vi utnyttjat att Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A+x_B=1} . Denna kurva är en rät linje som går mellan ångtrycken Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_B^*} (vid Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A=0} ) och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_A^*} (vid Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A=1} ).
Den andra kurvan är det totala ångtrycket som svarar mot ett givet molbråk Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_A} i ångan (för att den ska stå i jämvikt med vätskan). Detta ångtryck ges av:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_{tot}=\frac{p_A^*\,p_B^*}{p_A^*+(p_B^*-p_A^*)y_A}}
och kan också tolkas som det minimala tryck man behöver lägga på en gas med en viss sammansättning för att den ska börja kondensera.
Ett exempel visas i figuren nedan. Diagrammet kan avläsas på följande sätt. Vi startar med en vätskeblandning med molbråket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A=0.4} . Den blå linjen (vätskelinjen) visar ångtrycket över en sådan blandning (Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_{tot}} ). Om vi drar en horisontell linje vid detta tryck kan vi vid den gröna kurvan avläsa vilket molbråk i ångan som svarar mot detta ångtryck, i detta fall Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_A=0.65} . Detta är alltså ångans sammansättning över en viss vätskeblandning och vi ser att ångan har en större andel av den mest lättflyktiga komponenten A (alltså den komponent med högst ångtryck för det rena ämnet).
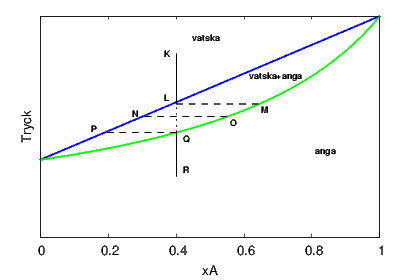
Samma diagram kan också tolkas som ett fasdiagram. Vi låter då x-axeln beteckna den totala sammansättningen i systemet ("det vi lagt i") och y-axeln det trycket vi lägger på (kom ihåg att temperaturen hela tiden är fastlåst till en konstant). Diagrammet visar då, för en given totalsammansättning och totaltryck huruvida systemet befinner sig i gasfas (under gaslinjen), vätskefas (över vätskelinjen) eller i tvåfasområdet med både vätska och gas (området mellan linjerna). Ett exempel visas nedan.
Låt oss i diagrammet följa ett system med totalsammansättningen Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_A=0.4, x_B=0.6} , som från början är under tillräckligt högt tryck för att vara en vätskeblandning (punkt K i figuren nedan). Om vi gradvis minskar det pålagda trycket kommer ingenting att hända förrän vi kommer till vätskelinjen (punkt L). Där börjar blandningen att koka och ångan får inledningsvis molbråket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_A=0.65} . Vi förbinder därför punkterna L och M med en "tie line", vars ändpunkter visar sammansättningen av de två faser vi har i systemet. Om vi fortsätter att minska trycket kommer både vätskans och ångans sammansättning att förändras enligt respektive linje (punkterna N och O). Samtidigt som både vätskan och ångan blir mer rika på B så ökar andelen gas i systemet, så att den totala sammansättningen inte förändras. När vi kommer fram till punkten P så förångas den sista vätskan, och fortsätter vi sänka trycket har vi en homogen gasblandning med sammansättningen Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_A=0.4} .
Fasdiagram (temperatur mot sammansättning)
I de ovanstående diagrammen avsatte vi trycket på y-axeln medan vi höll temperaturen konstant. Ännu mer användbart blir diagrammen om man istället avsätter temperaturen på y-axeln medan man håller trycket konstant. Sådana diagram visas i figur 5C.5 och 5C.6 i Chemical principles. Notera att diagrammen fortfarande kan tolkas på två sätt:
- för att avläsa kokpunkt och ångans sammansättning för en given vätskelösning (vilket de gör i boken)
- som fasdiagram som talar om vilken fas (eller vilka faser) som finns vid en given temperatur och totalsammansättning
Notera också att om den "undre" blå linjen kallas för kokpunktslinje, så skulle den "övre" röda linjen kunna kallas för kondensationspunktslinje, eftersom den, för ånga med given sammansättning, talar om vid vilken temperatur ångan börjar kondensera. För rena ämnen är förstås kokpunkten och kondensationspunkten samma temperatur, men detta gäller alltså inte för blandningar.
Avvikelse från ideal lösning
Tidigare definierade vi aktiviten Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} (en sorts effektiv koncentration) för ett godtyckligt system genom dess enkla samband med den kemiska potentialen:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_i=\mu_i^\circ + RT\ln a_i}
Vi har sett att för ideala vätskelösningar gäller
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i=x_i}
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i} är molbråket i vätskan. Det är därför naturligt att för rimliga avvikelser från idealt beteende införa en korrektion till detta uttryck, som brukar kallas aktivitetsfaktor eller aktivitetskoefficient och betecknas Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma_i} för en viss komponent i. Det är viktigt att förstå att denna aktivitetsfaktor oftast är olika för de olika komponenterna i lösningen. Vi skriver alltså:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i=\gamma_i\,x_i}
Vi kan kombinera detta med uttrycket för kemiska potentialen och ser då att aktivitetsfaktorn ger ett additivt bidrag till den kemiska potentialen (se t.ex. handledningen för destillationslabben):
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_i=\mu_i^\circ + RT\ln x_i + RT\ln \gamma_i}
När Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma_A>1} talar vi om en positiv avvikelse från Raoults lag (för en viss komponent A). Partialtrycket av komponenten är då större än det hade varit över en ideal lösning och vi kan dra slutsatsen att A-molekylerna "trivs sämre" i lösningen än de gör i det rena ämnet, vilket ofta innebär att de har mindre attraktiva interaktioner med de övriga molekylslagen i lösningen. Omvänt, när Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma_A<1} talar vi om en negativ avvikelse från Raoults lag. Partialtrycket av komponenten är då mindre än det hade varit över en ideal lösning och vi kan dra slutsatsen att A-molekylerna "trivs bättre" i lösningen än de gör i det rena ämnet. Ofta, men inte alltid, visar alla komponenterna i lösning samma sorts avvikelse från idealitet, men avvikelsens storlek kan variera kraftigt. Exempel hur det totala ångtrycket kan variera med vätskans sammansättning för de två olika fallen visas i figur 5C.9 i Chemical principles.
Om avvikelserna från idealitet är stora kan vi få ett kokpunktsminimum (om det är positiv avvikelse) eller ett kokpunktsmaximum (om det är negativ avvikelse). Detta illustreras i figur 5C.10 och 5C.11 i Chemical principles, men tyvärr har de blandat ihop linjerna i figur 5C.11: den understa är alltid kokpunktslinjen. Den punkt där kokpunkten har ett maximum eller minimum, och där ångans sammansättning är densamma som vätskans, kallas för azeotrop. Effekten av azeotroper på destillationsprocesser diskuteras i boken.