Skillnad mellan versioner av "Gibbs energi och kemisk potential"
Per (Diskussion | bidrag) m (Per flyttade sidan Kemisk potential till Gibbs energi och kemisk potential utan att lämna en omdirigering) |
Per (Diskussion | bidrag) (→Tryckberoende) |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 9: | Rad 9: | ||
== Temperaturberoende == | == Temperaturberoende == | ||
| − | Temperaturberoendet beskrivs i Chemical principles, först för rena ämnen i avsnitt 4J.1 och sedan för kemiska reaktioner i avsnitt 4J.4. Det mest lättöverskådliga exemplet är när vi jämför Gibbs energi (per mol) för olika faser av samma ämne för ett givet tryck (figur 4J.3 och 4J.4). Eftersom den molära entropin är minst för fast fas och störst för gasfas, kommer den negativa lutningen på ''G<sub>m</sub>''-kurvan (vilken approximativt är en rät linje) också att vara minst för fast fas och störst för gasfas. Detta leder till att kurvorna skär varandra, d.v.s. att vi får en temperatur där fast fas och vätska har samma ''G<sub>m</sub>'' (smältpunkten) och motsvarande för vätska och gasfas (kokpunkten). Det kan också inträffa att vätskan aldrig har lägst 'G<sub>m</sub>'' för det givna trycket (se figur 4J.4), och då får vi istället en sublimeringspunkt där fast fas och gas har samma ''G<sub>m</sub>''. | + | Temperaturberoendet beskrivs i Chemical principles, först för rena ämnen i avsnitt 4J.1 och sedan för kemiska reaktioner i avsnitt 4J.4. Det mest lättöverskådliga exemplet är när vi jämför Gibbs energi (per mol) för olika faser av samma ämne för ett givet tryck (figur 4J.3 och 4J.4). Eftersom den molära entropin är minst för fast fas och störst för gasfas, kommer den negativa lutningen på ''G<sub>m</sub>''-kurvan (vilken approximativt är en rät linje) också att vara minst för fast fas och störst för gasfas. Detta leder till att kurvorna skär varandra, d.v.s. att vi får en temperatur där fast fas och vätska har samma ''G<sub>m</sub>'' (smältpunkten) och motsvarande för vätska och gasfas (kokpunkten). Det kan också inträffa att vätskan aldrig har lägst ''G<sub>m</sub>'' för det givna trycket (se figur 4J.4), och då får vi istället en sublimeringspunkt där fast fas och gas har samma ''G<sub>m</sub>''. |
När vi tittar på jämvikt så kommer vi dessutom behöva temperaturberoendet av kvoten G/T. Den beskrivs av Gibbs-Helmholtz ekvation: | När vi tittar på jämvikt så kommer vi dessutom behöva temperaturberoendet av kvoten G/T. Den beskrivs av Gibbs-Helmholtz ekvation: | ||
:<math>\left(\frac{\partial (G/T)}{\partial T}\right)_p=-\frac{H}{T^2}</math> | :<math>\left(\frac{\partial (G/T)}{\partial T}\right)_p=-\frac{H}{T^2}</math> | ||
| − | |||
== Tryckberoende == | == Tryckberoende == | ||
| Rad 26: | Rad 25: | ||
vilket kan integreras från ett referenstryck <math>p^0</math> till det tryck <math>p^f</math> som vi är intresserade av: | vilket kan integreras från ett referenstryck <math>p^0</math> till det tryck <math>p^f</math> som vi är intresserade av: | ||
| − | :<math>G_m(p)=G_m(p^0) + \int_{p^0}^{p^f} V_m\,dp</math> | + | :<math>G_m(p^f)=G_m(p^0) + \int_{p^0}^{p^f} V_m\,dp</math> |
Detta uttryck gäller för alla faser av ett ämne, men för att beräkna integralen behöver vi veta hur molvolymen <math>V_m</math> beror på trycket. | Detta uttryck gäller för alla faser av ett ämne, men för att beräkna integralen behöver vi veta hur molvolymen <math>V_m</math> beror på trycket. | ||
| Rad 34: | Rad 33: | ||
Molvolymen för en kondenserad fas ändras bara marginellt när trycket ökar (eftersom molekylerna redan är i "kontakt" med varandra). Vi kan därför behandla <math>V_m</math> som en konstant och flytta den utanför integralen: | Molvolymen för en kondenserad fas ändras bara marginellt när trycket ökar (eftersom molekylerna redan är i "kontakt" med varandra). Vi kan därför behandla <math>V_m</math> som en konstant och flytta den utanför integralen: | ||
| − | :<math>G_m(p)=G_m(p^0) + V_m\,\int_{p^0}^{p^f}\, dp=G_m(p^0)+V_m\cdot(p^f-p^0)</math> | + | :<math>G_m(p^f)=G_m(p^0) + V_m\,\int_{p^0}^{p^f}\, dp=G_m(p^0)+V_m\cdot(p^f-p^0)</math> |
Vid normala förhållanden är termen <math>V_m\cdot(p^f-p^0)</math> mycket liten och kan försummas. Vi brukar därför anta att Gibbs energi för fasta ämnen och vätskor är oberoende av trycket. Men om vi är intresserade av geofysiska problem där trycket i berggrunden kan bli väldigt stort, kan man behöva ta hänsyn till tryckberoendet. Ett exempel är uppgift K17 där man ska beräkna hur stort tryck som krävs för att ändra vilken form av kol (grafit eller kol) som är mest termodynamiskt stabil. | Vid normala förhållanden är termen <math>V_m\cdot(p^f-p^0)</math> mycket liten och kan försummas. Vi brukar därför anta att Gibbs energi för fasta ämnen och vätskor är oberoende av trycket. Men om vi är intresserade av geofysiska problem där trycket i berggrunden kan bli väldigt stort, kan man behöva ta hänsyn till tryckberoendet. Ett exempel är uppgift K17 där man ska beräkna hur stort tryck som krävs för att ändra vilken form av kol (grafit eller kol) som är mest termodynamiskt stabil. | ||
| Rad 42: | Rad 41: | ||
Eftersom molvolymen för gaser beror starkt på trycket så kan vi inte hantera den som en konstant i integralen. Om vi antar att gasen är ideal kan vi istället sätta in <math>V_m=RT/p</math> och därmed, eftersom <math>T</math> är konstant, finna: | Eftersom molvolymen för gaser beror starkt på trycket så kan vi inte hantera den som en konstant i integralen. Om vi antar att gasen är ideal kan vi istället sätta in <math>V_m=RT/p</math> och därmed, eftersom <math>T</math> är konstant, finna: | ||
| − | :<math>G_m(p)=G_m(p^0) + RT\,\int_{p^0}^{p^f}\, \frac{1}{p}\,dp=G_m(p^0)+RT\ln\frac{p^f}{p^0}</math> | + | :<math>G_m(p^f)=G_m(p^0) + RT\,\int_{p^0}^{p^f}\, \frac{1}{p}\,dp=G_m(p^0)+RT\ln\frac{p^f}{p^0}</math> |
Detta uttryck visar exempelvis att när trycket tiodubblas vid rumstemperatur, ökar Gibbs molära energi med <math>RT\ln 10\approx 6</math> kJ/mol. I praktiken använder vi ovanstående uttryck även för icke-ideala gaser om de inte har extrema tryck. Om vi kallar Gibbs molära energi vid standardtrycket <math>p^0=1</math> bar för <math>G^0</math> kan vi alltså skriva Gibbs energi för en gas vid godtyckligt tryck: | Detta uttryck visar exempelvis att när trycket tiodubblas vid rumstemperatur, ökar Gibbs molära energi med <math>RT\ln 10\approx 6</math> kJ/mol. I praktiken använder vi ovanstående uttryck även för icke-ideala gaser om de inte har extrema tryck. Om vi kallar Gibbs molära energi vid standardtrycket <math>p^0=1</math> bar för <math>G^0</math> kan vi alltså skriva Gibbs energi för en gas vid godtyckligt tryck: | ||
:<math>G_m(p)=G^0 + RT\ln\frac{p}{p^0}</math> | :<math>G_m(p)=G^0 + RT\ln\frac{p}{p^0}</math> | ||
| − | |||
== Kemisk potential == | == Kemisk potential == | ||
Nuvarande version från 15 november 2017 kl. 11.10
Enligt fundamentalekvationerna kan en liten ändring i Gibbs energi för ett enkomponentsystem skrivas
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dG=V\,dp-S\,dT}
vilket också kan uttryckas som två partiella derivator:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S}
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V}
Innehåll
Temperaturberoende
Temperaturberoendet beskrivs i Chemical principles, först för rena ämnen i avsnitt 4J.1 och sedan för kemiska reaktioner i avsnitt 4J.4. Det mest lättöverskådliga exemplet är när vi jämför Gibbs energi (per mol) för olika faser av samma ämne för ett givet tryck (figur 4J.3 och 4J.4). Eftersom den molära entropin är minst för fast fas och störst för gasfas, kommer den negativa lutningen på Gm-kurvan (vilken approximativt är en rät linje) också att vara minst för fast fas och störst för gasfas. Detta leder till att kurvorna skär varandra, d.v.s. att vi får en temperatur där fast fas och vätska har samma Gm (smältpunkten) och motsvarande för vätska och gasfas (kokpunkten). Det kan också inträffa att vätskan aldrig har lägst Gm för det givna trycket (se figur 4J.4), och då får vi istället en sublimeringspunkt där fast fas och gas har samma Gm.
När vi tittar på jämvikt så kommer vi dessutom behöva temperaturberoendet av kvoten G/T. Den beskrivs av Gibbs-Helmholtz ekvation:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\partial (G/T)}{\partial T}\right)_p=-\frac{H}{T^2}}
Tryckberoende
Eftersom volymen är ett positivt tal för alla ämnen, ökar Gibbs energi alltid med trycket. Eftersom den molära volymen är större för gaser än för kondenserade faser (fast ämne och vätska), är Gibbs molära energi för en gas mer känslig för tryckändringar än för kondenserade faser.
För att hitta explicita formler för tryckberoendet håller vi temperaturen konstant och räknar på 1 mol av ämnet. Fundamentalekvationen förenklas då till
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dG_m=V_m\,dp\;\;\;\;\;\;} (konstant temperatur)
vilket kan integreras från ett referenstryck Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p^0} till det tryck Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p^f} som vi är intresserade av:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m(p^f)=G_m(p^0) + \int_{p^0}^{p^f} V_m\,dp}
Detta uttryck gäller för alla faser av ett ämne, men för att beräkna integralen behöver vi veta hur molvolymen Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_m} beror på trycket.
Kondenserad fas (fast eller vätska)
Molvolymen för en kondenserad fas ändras bara marginellt när trycket ökar (eftersom molekylerna redan är i "kontakt" med varandra). Vi kan därför behandla Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_m} som en konstant och flytta den utanför integralen:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m(p^f)=G_m(p^0) + V_m\,\int_{p^0}^{p^f}\, dp=G_m(p^0)+V_m\cdot(p^f-p^0)}
Vid normala förhållanden är termen Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_m\cdot(p^f-p^0)} mycket liten och kan försummas. Vi brukar därför anta att Gibbs energi för fasta ämnen och vätskor är oberoende av trycket. Men om vi är intresserade av geofysiska problem där trycket i berggrunden kan bli väldigt stort, kan man behöva ta hänsyn till tryckberoendet. Ett exempel är uppgift K17 där man ska beräkna hur stort tryck som krävs för att ändra vilken form av kol (grafit eller kol) som är mest termodynamiskt stabil.
Gas
Eftersom molvolymen för gaser beror starkt på trycket så kan vi inte hantera den som en konstant i integralen. Om vi antar att gasen är ideal kan vi istället sätta in Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_m=RT/p} och därmed, eftersom Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} är konstant, finna:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m(p^f)=G_m(p^0) + RT\,\int_{p^0}^{p^f}\, \frac{1}{p}\,dp=G_m(p^0)+RT\ln\frac{p^f}{p^0}}
Detta uttryck visar exempelvis att när trycket tiodubblas vid rumstemperatur, ökar Gibbs molära energi med Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle RT\ln 10\approx 6} kJ/mol. I praktiken använder vi ovanstående uttryck även för icke-ideala gaser om de inte har extrema tryck. Om vi kallar Gibbs molära energi vid standardtrycket Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p^0=1} bar för Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G^0} kan vi alltså skriva Gibbs energi för en gas vid godtyckligt tryck:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m(p)=G^0 + RT\ln\frac{p}{p^0}}
Kemisk potential
Kemisk potential är ett kraftfullt verktyg när vi resonerar om fasjämvikter, kemiska jämvikter och blandningar. Chemical principles nosar bara på detta när de använder "molär Gibbs energi" för att beskriva fasjämvikt i den gula rutan på sidan 352, samt kemisk jämvikt i avsnitt 5G.4.
När vi har flera komponenter (molekylslag) i ett system måste fundamentalekvationerna utökas för att kunna beskriva ändringar i den kemiska sammansättningen som sker via exempelvis kemiska reaktioner. Om vi koncentrerar oss på Gibbs energi får vi
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dG=V\,dp-S\,dT + \sum_i \mu_i\, dn_i\;\;\;\;\;\;\;\;\;\;} (1)
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_i} är den kemiska potentialen för ämne i och Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dn_i} är en liten ändring av substansmängden av ämnet. Den kemiska potentialen kan tolkas som ett ämnes benägenhet att "fly" eller "reagera". Den kan liknas vid den elektriska potentialen som beskriver en positiv laddnings benägenhet att fly undan från en plats. Precis som den elektriska potentialen kan den kemiska potentialen för ett ämne i princip variera i rummet, vilket gör att man kan beskriva diffusion och koncentrationsgradienter. I termodynamik för bulksystem är den dock konstant i hela systemet, både inom en fas och, som vi snart ska se, mellan olika faser.
En annan analogi kan göras med mekanikens potentiella energi per kg (även kallad gravitationspotential). En hög potentiell energi innebär en hög förmåga att utföra arbete. På samma sätt kan vi, om vi antar konstant tryck och temperatur, beräkna det reversibla extraarbetet (utöver tryck-volymsarbete) för en kemisk reaktion med hjälp av de kemiska potentialerna:
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle w_{extra,rev}=dG=\sum_i \mu_i\, dn_i}
Detta är direkt tillämpbart vid konstruktion av galvaniska celler (batterier och bränsleceller).
Definition av kemisk potential
Ur ekvation (1) ovan kan vi direkt utläsa en explicit definition av den kemiska potentialen för ett ämne A: (det finns flera ekvivalenta definitioner, en för varje fundamentalekvation)
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_A=\left(\frac{\partial G}{\partial n_A}\right)_{p,T,n\prime}}
där Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n\prime} indikerar att substansmängden av alla övriga komponenter ska hållas konstanta, tillsammans med tryck och temperatur.
För ett system med en enda komponent (d.v.s. ett rent ämne) är den kemiska potentialen exakt samma sak som den molära Gibbs energin (Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m} ). Detta kan lätt inses genom att Gibbs energi för ett ämne är en extensiv storhet som är proportionell mot mängden, Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G=n\cdot G_m} , och derivatan av Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G} med avseende på Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} är förstås Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_m} .
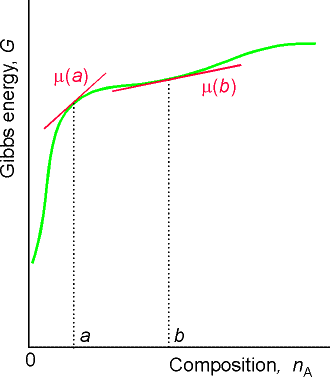
För blandningar blir definitionen med partiell derivata mer intressant, eftersom Gibbs energi då inte behöver ändras linjärt med mängden (se t.ex. figuren ovan). Den kemiska potentialen kallas även partiell molär Gibbs energi och tillhör en grupp storheter som kallas partiella molära storheter, vilka lite grovt kan sägas beskriva hur stor del av en storhet som utgörs av en komponent i en blandning. Vi kan på samma sätt definiera den partiella molära volymen för ett ämne A i en blandning som
- Misslyckades med att tolka (MathML med SVG- eller PNG-återgång (rekommenderas för moderna webbläsare och tillgänglighetsverktyg): Ogiltigt svar ("Math extension cannot connect to Restbase.") från server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_A=\left(\frac{\partial V}{\partial n_A}\right)_{p,T,n\prime}}
Den partiella molära volymen talar alltså om hur mycket volymen ökar om man tillsätter en liten mängd av ämnet till en blandning, vilket inte behöver vara detsamma som volymen av motsvarande mängd rent ämne. Exempelvis är molvolymen för rent vatten 18 cm3/mol, men om vi adderar 1 mol vatten till en stor volym av ren etanol ökar volymen bara med 14 cm3 p.g.a. vattenmolekylerna i viss utsträckning kan packas in mellan etanolmolekylerna. Den partiella molära volymen av vatten i ren etanol är alltså 14 cm3/mol.